OCT technology

Fundamental technical principle

As indicated by its acronym, optical coherence tomography (OCT) is a technology that incorporates several key principles:

  • Optical: It employs light waves for imaging.
  • Coherence: The technique utilizes the principle of low-coherence interferometry.
  • Tomography: OCT provides cross-sectional information about the sample being imaged.

    • In a classic Michelson interferometer setup shown here, when a narrowband light source emits a coherent beam that is split into two paths by a beam splitter. One beam is reflected off a fixed reference mirror, while the other reflects off a movable sample mirror. The difference in the optical path lengths of the two beams, denoted as Δz, changes as a result of translational movement of the sample mirror. 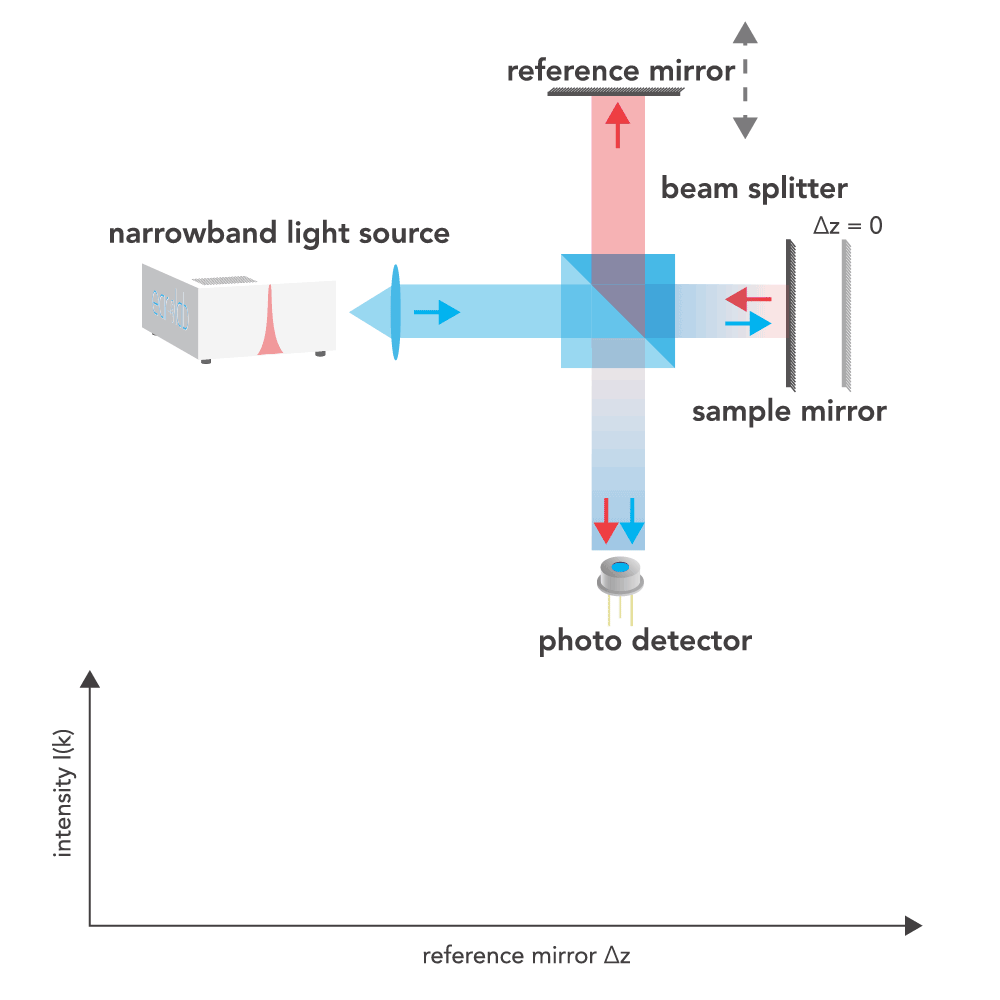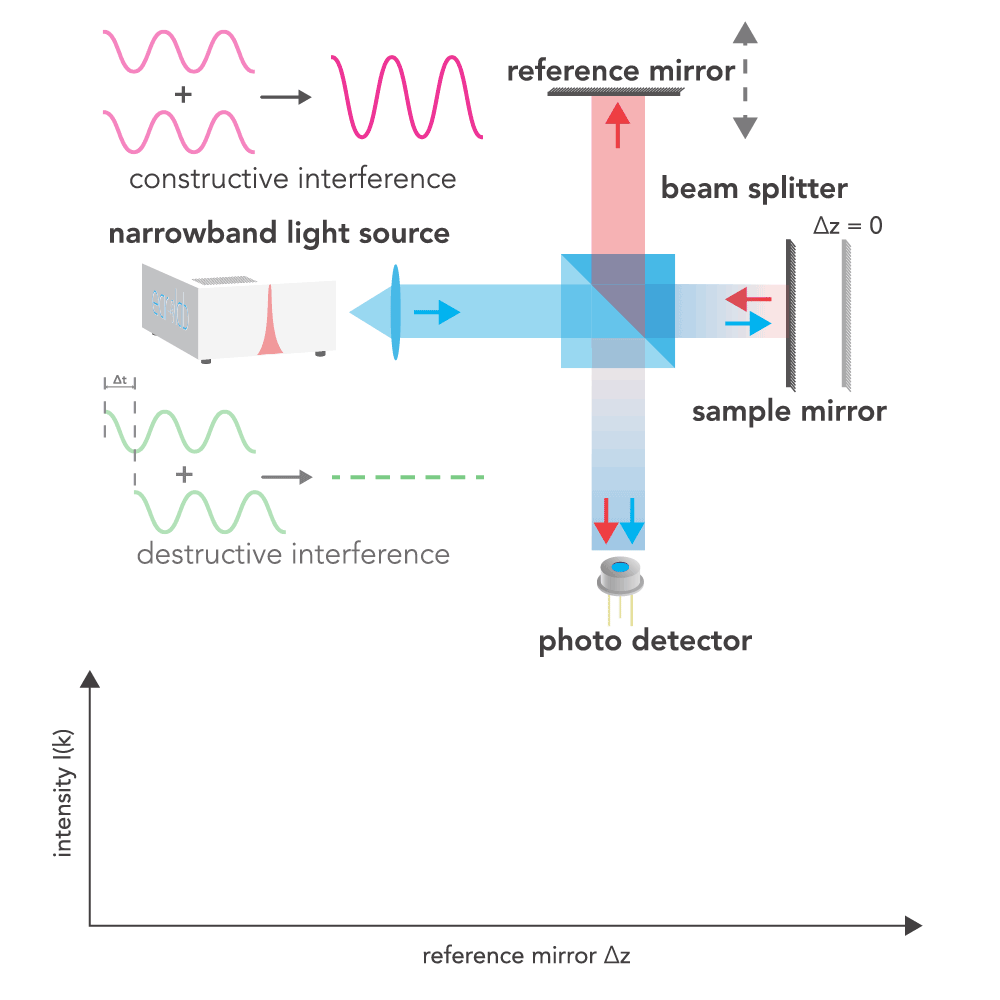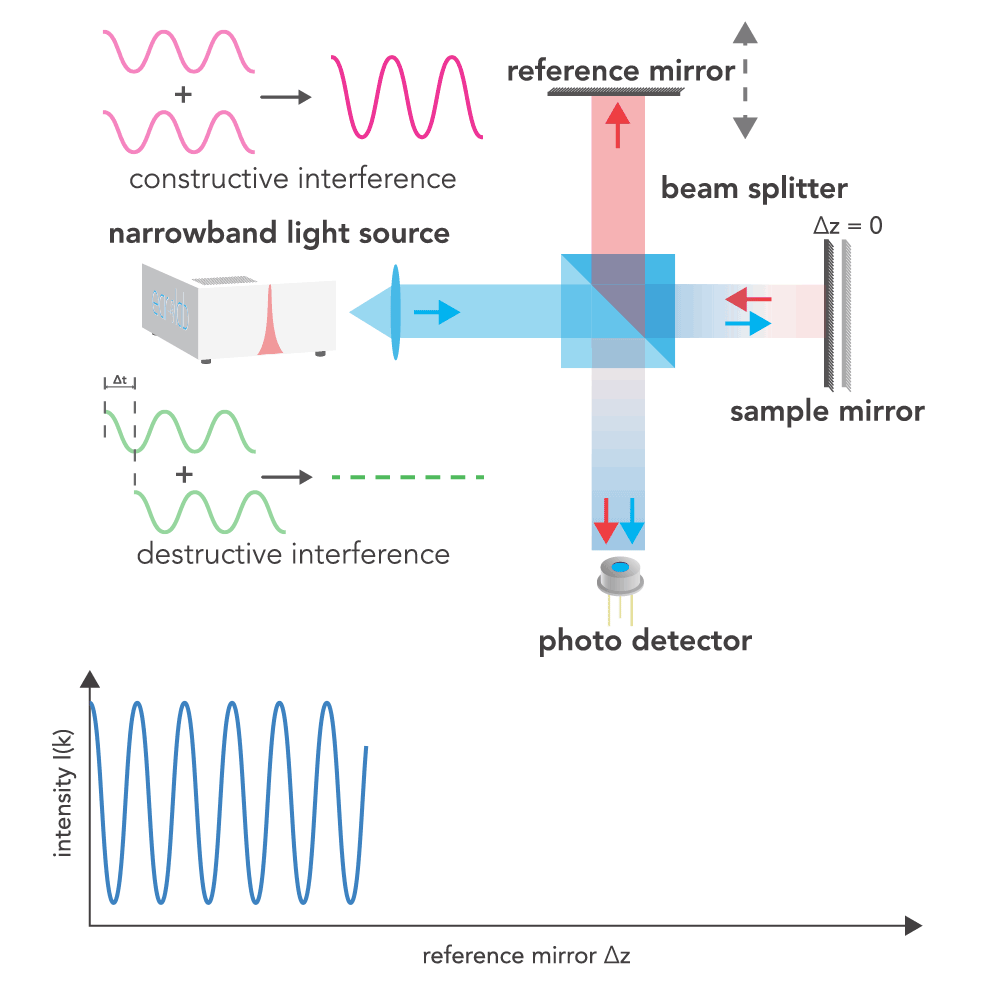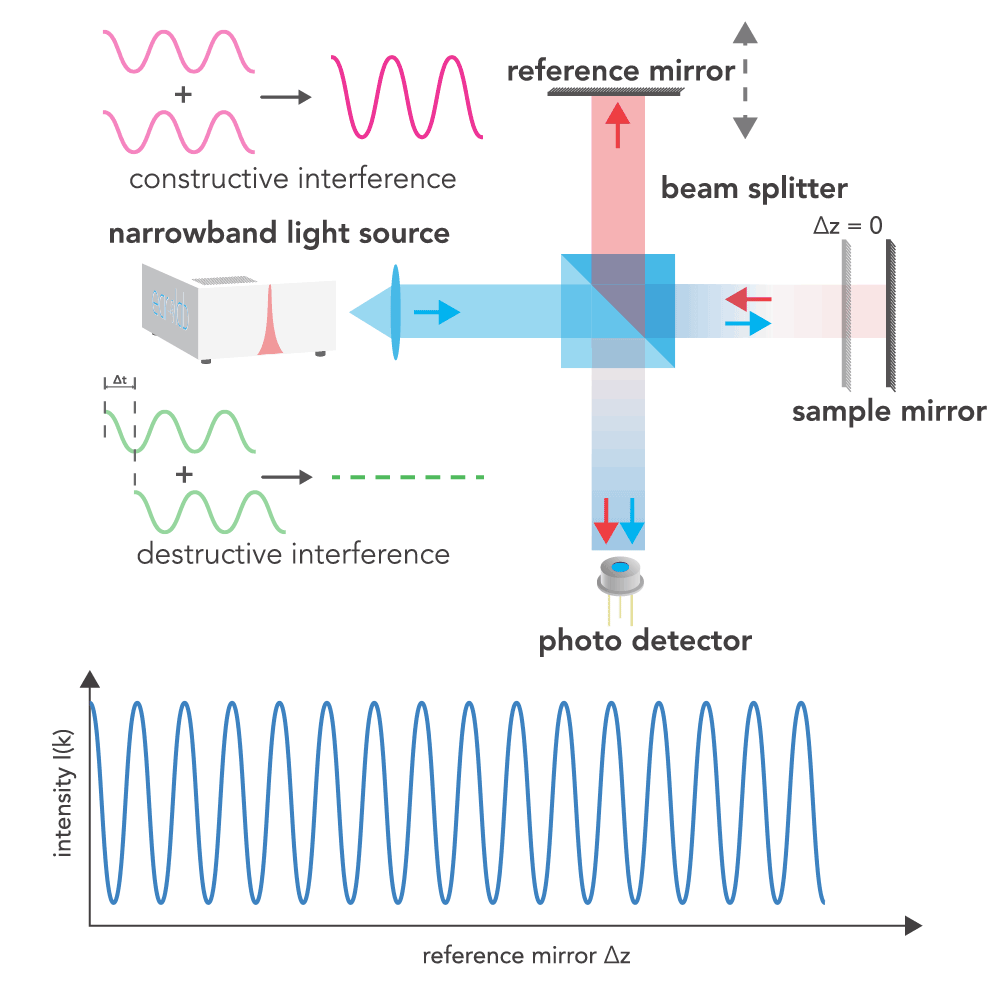The beams are recombined at the beam splitter, which results an interference pattern that is then detected by a photodetector. This interference pattern is essentially the superposition of light reflected from both the reference mirror and the sample mirror. When the peaks of the two light waves align, constructive interference occurs, leading to an increase in intensity. Conversely, when there is a mismatch such that the peaks of one wave align with the troughs of another, destructive interference occurs, resulting in a reduction or cancellation of intensity.

    Interferometry extracts information from the interference of superimposed waves from two arms.

    Elaborating on the principle of low-coherence interferometry, OCT uses utilises low-coherence or partially coherent light to localise structures by correlating interfering light that is back-scattered from the sample arm, \(E_s\), with the light reflected from the reference arm, \(E_r\).


    In OCT, a photodetector measures the intensity of the interfered light \(I_o\), which is proportional to the total electrical field as described by its relationship \( I = |E|^2 \).

    \( I_0 \sim \langle E_r E_r^* \rangle + \langle E_s E_s^* \rangle + E_s E_r^* e^{-i2k(\Delta l)} + E_r E_s^* e^{-i2k(\Delta l)} \)

    The term \( E_r E_r^* \), often referred to as the "DC" term, is the time average of the square of the electric fields or irradiance of the light from the reference arm and represents the dominant component in the detector current. The expression \( E_r E_r^* \) is independent of sample reflectivity and optical pathlength difference \( \Delta l \). The autocorrelation term \( E_s E_s^* \), describes the interference caused by multiple reflectors present within the sample. In conventional OCT, this interference is a source of unwanted artifacts, but it can be minimized by ensuring that the reference intensity is much higher than the sample intensity. The terms of interest, the cross-correlation term \( E_s E_r^* e^{-i2k(\Delta l)} + E_r E_s^* e^{-i2k(\Delta l)} \), depend on the intensity in the sample and reference arms, the path length difference between the sample and reference arms, and the sample reflectivity. To ensure that this desired term is larger than the undesired autocorrelation term \( E_s E_s^* \), the system is designed such that \( |E_r| \gg |E_s| \). Some authors describe the relative increase in the cross-correlation term as compared to the autocorrelation term in terms of a “gain” applied to the sample signal by the reference arm signal.